THE SECRET OF ODT PROBLEMS, by Ofer Comay

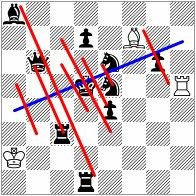
Every helpmate composer noticed that some problems show ODT (Orthogonal Diagonal Transformation) features with amazingly precise appearance. No.1 is a good illustration. If you compare the two solutions, you see that every diagonal move in the first phase becomes an orthogonal move in the second phase, and vise versa. Not only this, but every diagonal motif in one phase becomes an orthogonal motif in the second phase, and vise versa. There are plenty of ODT problems that show such exact match of moves and motifs, and this article will show the mechanism that enables such problems.

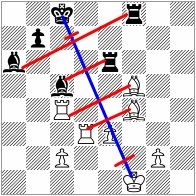
During one of the congresses Vlaicu Crisan showed me a problem of his, No.2. If you follow this problem, you can see a fantastic rich combination, showing two Grimshaw's on e3 and d6, with 8 thematic lines. I remember that this striking problem caused me to start thinking: "Why such amazing combinations exist? Is there a mathematical rule which allows such combinations?" But it was 2 AM after midnight and this question waited for two more years.

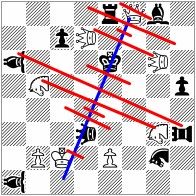
While I was composing No.3 for the 9th WCCT, I wrote to my friend that I found an "enchanted" scheme - everything I tried works much better than I could imagine. The problem shows a cyclic shift of the anti-battery piece and critical squares, it contains 12 thematic lines, some of them are Nao (Chinese knight) lines, with perfect ODT. After achieving this scheme, I asked myself again if there is a rule which enables such problems. I noticed the two triangles g6-a6-d3 and d7-h3-d3 have almost the same area. For me this was the key that helped exposing the rule that makes such problems possible.

I will start with simply showing how it works, and then provide the boring explanation about why it works. Then we will see how this rule was used in the past, probably unintentionally, and finish with couple of philosophical questions.

The ODT symmetry rule

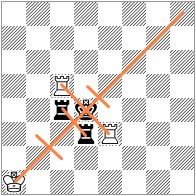
Look again on problem No.1. Lets draw a straight line from h7 to a4. This is the symmetry line. You will see that every piece in one side of the symmetry line has a corresponding piece on the other side, except that bishop is mapped to rooks and rooks to bishops. In No.1 Qb6 is used as a bishop and its mirror piece is Rc3. Not only that, but every square and every line in one solution appear in the symmetrical solution. There is a slightly asymmetrical usage of Bf7 and Rh5 which can be "corrected" if we move Rh5 to g5. This kind of symmetry breaking is not really a break because the pieces are used effectively in a symmetrical way.

No.2 has a symmetry line from f1 to c8, and No.3 from c1 to f8.

No1. explained h#3 b) Pe4->d6 (3+10)

No2. explained hs#4 2 solutions (8+6)

No3. explained hs#4 b) Kc2->d2 (8+10)

The explanation to the ODT symmetry

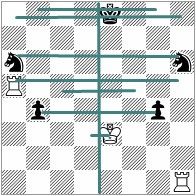
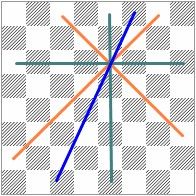
The mathematical explanation is amazingly simple, and it is hard to understand how we, the composers, used it so many years without noticing it. Let's start with known symmetries as we see in No.4 (vertical symmetry) and No.5 (diagonal symmetry). I put few pieces intentionally on squares that visually "breaks" the symmetry, but effectively they don't. We will see later that a similar phenomenon applies to ODT symmetry.

Now look in No.6. If we draw an imaginary line which goes exactly in the middle of the angle between an orthogonal line and diagonal line, then the symmetry takes every orthogonal line to diagonal line and vice versa. In No.6, the symmetry line is c1-f8, and, for example, the segment a6-e6 is mirrored to h3-e6, a2-e6 is mirrored to e1-e6, etc.

Obviously, this symmetry is not exact as the orthogonal or diagonal symmetry. For example, the square d5 can be mirrored to e5 or e4. The squares can be mapped in various ways, according to the context. Furthermore, even if one solution works, the ODT symmetrical solution doesn't automatically work: sometimes it is possible to use the symmetry, and sometimes it isn't. If this symmetry would be exact, then the value of a bishop in chess games would be equal to the value of a rook, but it isn't.

This "inaccurate" and "subjective" property of the ODT symmetry is probably the reason that we overlooked it so many years. As we will see in a moment, this rule plays an important role in many ODT problems. Many of them are great problems because this symmetry, unlike the other "trivial symmetries", is very pleasing and provides significant richness to the problems, while the trivial symmetries do not provide any additional content.

No4. Vertical symmetry h#2 b) Ke3->d3 (3+5)

No5. Diagonal symmetry h#2 2 solutions (3+3)

No6. ODT symmetry

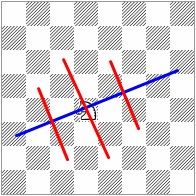
And why the knight works beautifully in this rule? We are lucky that a knight move is combined from an orthogonal move and a diagonal move, which makes a knight move rather close to the middle between these two, which is exactly the required symmetry line angle. See No.7 for the symmetry which is applied to the knight. See also No.8 how the ODT symmetry works regarding the flight squares of the king.

No7. Knight symmetry

No8. Flight symmetry

No. author source

We always used this rule, unintentionally

The ODT symmetry can appear in any problem type, but it is by far more common in helpmates or helpselfmates. Some composers use it quite often, like Gabor Cseh (nearly 30% of his H#2 and H#3 are ODT symmetrical), Mario Parrinello, Menachem Witztum and Vlaicu Crisan. Among the first 20 entries in the 9th WCCT fairy section, 8 problems were ODT symmetrical. I checked FIDE album 97-99 and found that 15% of the H#2 and H#3 were ODT symmetrical. I included in this article a selection of beautiful ODT symmetrical problems (see below NN.9 - 20 - editorial).

Is it possible to use this rule for composing?

Obviously yes. The last 2 problems (NN.19, 20 - editorial) in this article were composed after I found the ODT rule. Using this rule made the composing process faster and I knew what I was looking for. The problem with the grasshopper was composed intentionally in order to explore the possibilities with grasshopper, which is more difficult to use in ODT symmetrical problems compared to Chinese pieces. The reason is that a grasshopper must stand exactly one square behind the piece that was used for jumping, and the size of an orthogonal square is different than diagonal square.

The last question is rather interesting for us, as people who create art. Symmetry generally decreases the artistic value of a chess problem. In fact, the symmetrical solution doesn't add any additional value to the first, unless it is used as a try. Can we say that ODT symmetry also decreases the artistic value of the problem? I believe that the answer is negative, and the reason is that the symmetry doesn't work automatically, and it is subjective and applied according to the context. Furthermore, the "symmetrical" solution is not visually the same, and last, based on my experience, it is very difficult to compose good problems, even after knowing this rule. I spent an amazing number of hours composing the last two helpmates, and several others during the last couple of years.